Right-hand rule


The right-hand rule is a convention in vector math. It helps you remember direction when vectors get cross multiplied.
- Start by closing your right hand and stick out your pointer finger.
- Stick your thumb straight up as though you were making the sign for a gun.
- If you point your "gun" straight ahead, stick out your middle finger so that it points left and all your fingers are at right angles to each other.
If you have two vectors that you want to cross multiply, you can figure out the direction of the vector that comes out by pointing your thumb in the direction of the first vector and your pointer in the direction of the second vector. Your middle finger will point the direction of the cross product.
Remember that when you change the order that vectors get cross multiplied, the result goes in the opposite direction. So it's important to make sure that you go in the order of .
Variations[change | change source]
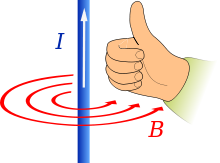
There is another rule called the right-hand grip rule (or corkscrew rule) that is used for magnetic fields and things that rotate.
- Start by putting your right hand out flat and point your thumb straight out so that it is at a right angle to your other fingers.
- Now curl your fingers into a fist and keep your thumb out (like a Thumbs Up).
- Match how your fingers curl in to the way something is moving. The direction that your thumb is pointing is the direction of the vector we use to talk about it.
You can do this in reverse by starting your thumb in the direction of the vector and see how your fingers curl to see the direction of rotation. If you point your thumb in the direction of current in a wire, the magnetic field that comes up around it is in the direction of your curling fingers.

