Snell's law
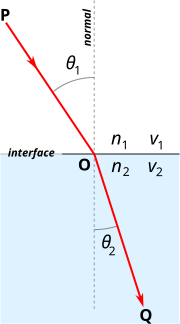

Snell's Law of Refraction is the scientific law of the refraction of light or other waves. In optics, Snell's law is about the speed of light in different media. The law states that when light passes through different materials (for example from air to glass) the ratio of sines of the incidence (incoming) angle and the refraction (outgoing) angle does not change:
With each as the angle measured from the normal of the boundary, as the velocity of light in the respective medium (SI units are meters per second, or m/s). is the refractive index of the medium.
The index of refraction of a vacuum is 1 and the velocity of light in a vacuum is . When a wave passes the material where the index of refraction is n, the velocity of the wave becomes .
Snell's law can be proved by Fermat's principle. Fermat's principle states that light travels along the path which takes the least time.
History[change | change source]
The idea has a long history. The problem had the attention of Hero of Alexandria, Ptolemy, Ibn Sahl, and Huygens. Ibn Sahl actually discovered the law of refraction.[1] In Traité de la Lumiere, 1678, Huygens showed how Snell's law of sines could be explained by, or derived from, the wave nature of light.[2]
References[change | change source]
- ↑ Kurt Bernardo Wolf 2004. Geometric optics on phase space, p. 9. Springer. ISBN 3-540-22039-9 online
- ↑ Rashed R. 1993. Géométrie et dioptrique au Xe siècle: Ibn Sahl, al-Quhi et Ibn al-Haytham. Paris: Les Belles Lettres.






