Time-domain spectroscopy
This article uses too much jargon, which needs explaining or simplifying. (January 2024) |
Time-domain spectroscopy is a type of spectroscopy that measures the power of electromagnetic radiation as a function of time. Normal spectroscopy is frequency-domain spectroscopy. It measures radiation as a function of frequency or wavelength. Time-domain spectroscopy usually requires the use of Fourier transforms.

Two monochromatic lights of different frequencies can combine to show interference patterns. At time t=0, the waves interfere constructively. This gives a maximum in the added plot. The waves get more out of phase. This leads to destructive interference and a minimum in the added plot. From one peak maximum to the next is a cycle. So when looking at two monochromatic lights, they can be graphed as two lines in the frequency-domain (this plot shows power, P(ν), as a function of frequency). The same two lights can be plotted as the sum of their waves in the time-domain (this plot shows power, P(t), as a function of time).

Absorptions in spectra usually look like broad peaks. This means that a peak may contain many wavelengths of radiation. These wavelengths can be plotted in the time domain. Notice that there are now smaller areas of constructive interference. This is because the closely spaced wavelengths quickly become more and more out of phase.
Getting time-domain spectra[change | change source]
Spectroscopy done with visible or infrared radiation involves wavelengths of 1012 to 1015 Hz. Phototransducers (instruments that convert light to information readable by a computer) cannot make measurements that quickly. What is needed is a way to make these high-frequency signals into low-frequency signals. For optical spectroscopy (such as infrared spectroscopy) the most common way to do this is by using a Michelson interferometer.
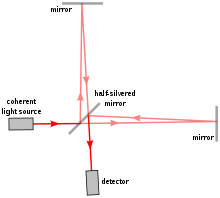
Monochromatic light traveling through a Michelson interferometer is split into two beams by a beam splitter. These beams travel to mirrors, reflect, and then recombine at the beam splitter. One of the mirrors can be moved. If the two mirrors are the same distance apart, they meet at the beam splitter in-phase and show constructive interference. As the one mirror is moved, the beams become slightly more out of phase. When the movable mirror has moved a distance equal to ¼ of the light's wavelength, the extra distance it travels is ½ the light's wavelength. This means that when the two beams combine at the beam splitter, they destructively interfere. So moving the mirror a total distance of ½ the wavelength of light means the spectra will show one complete cycle. One could then plot the power of radiation as a function of distance traveled by the movable mirror. However, by knowing the speed of the movable mirror the power of radiation can be plotted as a function of time.
Most time-domain spectroscopy experiments involve broadband radiation (radiation that consists of a large range of wavelengths).
Applications[change | change source]
Time-domain spectroscopy is used very often in infrared spectroscopy (FT-IR) and NMR spectroscopy(FT-NMR). It has several advantages over frequency-domain spectroscopy. In frequency-domain experiments, each wavelength must be measured one at a time. This means scans can take several minutes. A single time-domain experiment takes no longer than a minute. Usually it only takes seconds. This means that many scans may be taken for a given sample, and that the scans can be averaged. So not only is the time-domain experiment faster, but it can also have a better signal to noise ratio.
References[change | change source]
D.A. Skoog, F.J. Holler, S.R. Crouch. 2007. Principles of Instrumental Analysis. 6th ed, Thompson and Brooks/Cole: Canada.
