Convex set
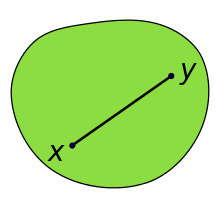

In Euclidean space, a region is a convex set if the following is true. For any two points inside the region, a straight line segment can be drawn. If every point on that segment is inside the region, then the region is convex.
The point is that a convex curve forms the boundary of a convex set. So, any shape which is concave, or has a hollow, cannot be a convex set.
Related pages[change | change source]
