Euler–Bernoulli beam theory

A vibrating glass beam showing the bending of beams which can be estimated using Euler-Bernoulli's beam theory.

Euler–Bernoulli beam theory (also known as engineer's beam theory or classical beam theory) is a simple method to calculate bending of beams when a load is applied. This applies to small deflections (how far something moves) of a beam without considering effects of shear deformations. Therefore, it can be considered a special case of the Timoshenko beam theory. It was first introduced around 1750. It gained popularity during the development of the Eiffel Tower and the Ferris wheel in the late 19th century. After that, it was used in many engineering fields including mechanical engineering and civil engineering. Although other advanced methods have been developed, the Euler-Bernoulli beam theory is still widely used because of its simplicity. 

History

Drawing of a cross section of a bent beam showing the neutral axis

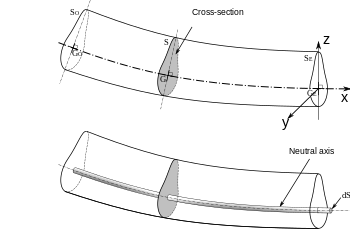
Leonhard Euler and Daniel Bernoulli were the first to put together the theory in 1750. At the time, science and engineering were viewed differently than today. Mathematical theories such as the Euler-Bernoulli Beam theory were not trusted for practical engineering use. Bridges and buildings continued to be designed using the same methods until the late 19th century. This is when the Eiffel Tower and Ferris wheel showed the validity of the theory on a larger scale.

Static beam equation

Bending of an Euler–Bernoulli beam. Each cross-section of the beam is at 90 degrees to the neutral axis.

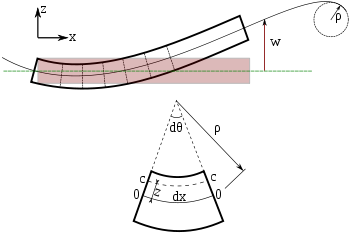
The Euler–Bernoulli equation describes the relationship between the beam's deflection and the applied load is as shown below:

${\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q\,$

Where $w(x)$ describes the deflection of the beam in the $z$ direction at some position $x$. $q$ is a distributed load, in other words a force per unit length (analogous to pressure being a force per area); it may be a function of $x$, $w$, or other variables.