Kruskal's algorithm
Kruskal's algorithm is a greedy algorithm to find a minimum spanning tree in a weighted, undirected graph. Joseph Kruskal first described it in 1956:
Perform the following step as many times as possible: Among the edges (..) not yet chosen, choose the shortest edge, which does not form any loops with those edges already chosen
— Kruskal, 1956[1]
In this case, the shortest edge is the one with the lowest weight.
Example[change | change source]
Download the example data. Archived 2012-07-16 at the Wayback Machine
| Image | Description |
|---|---|

|
AD and CE are the shortest edges, with length 5, and AD has been arbitrarily chosen, so it is highlighted. |

|
CE is now the shortest edge that does not form a cycle, with length 5, so it is highlighted as the second edge. |
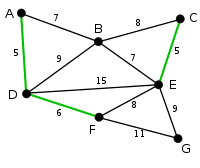
|
The next edge, DF with length 6, is highlighted using much the same method. |

|
The next-shortest edges are AB and BE, both with length 7. AB is chosen arbitrarily, and is highlighted. The edge BD has been highlighted in red, because there already exists a path (in green) between B and D, so it would form a cycle (ABD) if it were chosen. |
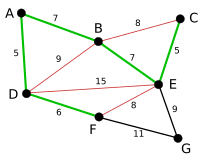
|
The process continues to highlight the next-smallest edge, BE with length 7. Many more edges are highlighted in red at this stage: BC because it would form the loop BCE, DE because it would form the loop DEBA, and FE because it would form FEBAD. |

|
Finally, the process finishes with the edge EG of length 9, and the minimum spanning tree is found. |
References[change | change source]
- ↑ Joseph. B. Kruskal (Feb 1956). "On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem" (PDF). Proceedings of the American Mathematical Society. 7 (1): 48–50. doi:10.1090/S0002-9939-1956-0078686-7. Archived from the original (PDF) on 2013-04-18. Retrieved 2012-12-11.
