Trigonometric function


In mathematics, the trigonometric functions are a set of functions which relate angles to the sides of a right triangle. There are many trigonometric functions, the 3 most common being sine, cosine, tangent, followed by cotangent, secant and cosecant.[1][2] The last three are called reciprocal trigonometric functions, because they act as the reciprocals of other functions. Secant and cosecant are rarely used.
| Function | Abbreviation | Relation (Radians) |
| Sine | sin | |
| Cosine | cos | |
| Tangent | tan (or tg) |
|
| Cotangent | cot (or ctg) |
|
| Secant | sec | |
| Cosecant | csc (or cosec) |
Definition[change | change source]
The trigonometric functions sometimes are also called circular functions. They are functions of an angle; they are important when studying triangles, among many other applications. Trigonometric functions are commonly defined as ratios of two sides of a right triangle containing the angle,[3] and can equivalently be defined as the lengths of various line segments from a unit circle (a circle with radius of one).
Right triangle definitions[change | change source]
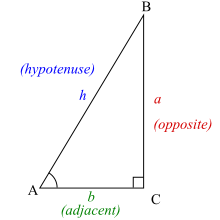
In order to define the trigonometric functions for the angle A, start with a right triangle that contains the angle A:
We use the following names for the sides of the triangle:
- The hypotenuse is the side opposite the right angle, also the longest side of a right-angled triangle, in this case h.
- The opposite side is the side opposite to the angle we are interested in, in this case a.
- The adjacent side is the side that is in contact with the right angle the angle we are interested in, hence its name. In this case, the adjacent side is b.
All triangles are taken to exist in Euclidean geometry, so that the inside angles of each triangle sum to π radians (or 180°); therefore, for a right triangle, the two non-right angles are between zero and π/2 radians. Notice that strictly speaking, the following definitions only define the trigonometric functions for angles in this range. We extend them to the full set of real arguments by using the unit circle, or by requiring certain symmetries and that they be periodic functions.
1) The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. In our case[3]
Note that since all those triangles are similar, this ratio does not depend on the particular right triangle that is chosen, as long as it contains the angle A.
The set of zeroes of sine (that is, the values of for which ) is
2) The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse. In our case[3]
The set of zeroes of cosine is
3) The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side. In our case[3]
The set of zeroes of tangent is
This is the same set as that of the sine function, since
The remaining three functions are best defined using the above three functions.
4) The cosecant csc(A) is the multiplicative inverse of sin(A); it is the ratio of the length of the hypotenuse to the length of the opposite side:[3]
- .
5) The secant sec(A) is the multiplicative inverse of cos(A); it is the ratio of the length of the hypotenuse to the length of the adjacent side:[3]
- .
6) The cotangent cot(A) is the multiplicative inverse of tan(A); it is the ratio of the length of the adjacent side to the length of the opposite side:
- .
Definitions by power series[change | change source]
One can also define the trigonometric functions by using power series:
and define tangent, cotangent, secant and cosecant using identities, see below.
Identities[change | change source]
Some important identities:
Hyperbolic functions[change | change source]
The hyperbolic functions are like the trigonometric functions, in that they have very similar properties. Each of six trigonometric functions has a corresponding hyperbolic form.[1] They are defined in terms of the exponential function, which is based on the constant e.
- Hyperbolic sine:
- Hyperbolic cosine:
- Hyperbolic tangent:
- Hyperbolic cotangent:
- Hyperbolic secant:
- Hyperbolic cosecant:
Related pages[change | change source]
References[change | change source]
- ↑ 1.0 1.1 "Comprehensive List of Algebra Symbols". Math Vault. 2020-03-25. Retrieved 2020-08-29.
- ↑ Weisstein, Eric W. "Trigonometric Functions". mathworld.wolfram.com. Retrieved 2020-08-29.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 "Sine, Cosine, Tangent". www.mathsisfun.com. Retrieved 2020-08-29.
- ↑ Weisstein, Eric W. "Cosine". mathworld.wolfram.com. Retrieved 2020-08-29.
Bibliography[change | change source]
- Joseph, George G., The Crest of the Peacock: Non-European Roots of Mathematics, 2nd ed. Penguin Books, London. (2000). ISBN 0-691-00659-8.
- "Madhava of Sangamagramma" Archived 2006-05-05 at the Wayback Machine, MacTutor History of Mathematics Archive. (2002).
- Weisstein, Eric W., "Tangent" from MathWorld, accessed 21 January 2006.
Other websites[change | change source]
- nanoSouffle Online Grapher Archived 2013-07-23 at the Wayback Machine - Extensible features for graphing functions... works in just about every browser, and JavaScript is simply a plus for real-time updates, and not a requirement.
- Sine and cosine function Archived 2002-05-31 at the Wayback Machine with an implementation in Rexx.
- Trigonomic Functions[permanent dead link] - An interactive sketch showing the trigonometric functions in terms of the unit circle.
- An excellent Flash animation for learning the unit circle




































