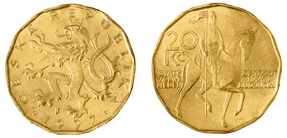Tridecagon
| Regular tridecagon | |
|---|---|
 A regular tridecagon | |
| Type | Regular polygon |
| Edges and vertices | 13 |
| Schläfli symbol | {13} |
| Coxeter diagram |    |
| Symmetry group | Dihedral (D13), order 2×13 |
| Internal angle (degrees) | ≈152.308° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
A tridecagon or triskaidecagon or trisdecagon or 13-gon is a shape with 13 sides and 13 corners.
Regular tridecagon[change | change source]
All sides of a regular tridecagon are the same length. Each corner is 147.27°. All corners added together equal 6840°.
Area[change | change source]
The amount of space a regular tridecagon takes up is
a is the length of one of its sides.
Numismatic use[change | change source]
The regular tridecagon is used as the shape of the Czech 20 korun coin.[1]
Related pages[change | change source]
References[change | change source]
- ↑ Colin R. Bruce, II, George Cuhaj, and Thomas Michael, 2007 Standard Catalog of World Coins, Krause Publications, 2006, ISBN 0896894290, p. 81.
Other websites[change | change source]
- Eric W. Weisstein, Tridecagon at MathWorld.
Special cases, including regular polygons with their own names, in parentheses List of polygons by number of sides | ||
| 1–10 sides |  | |
| 11–20 sides | ||
| 21–30 sides | ||
| 31–50 sides | ||
| 51–100 sides (selected) | ||
| >100 sides | ||
| Star polygons (5–12 sides) | ||
| Triangles | ||
| Quadrilaterals | ||
