Square root of 2
(Redirected from Square root of two)
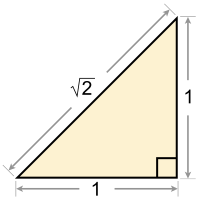
The square root of 2, or the (1/2)th power of 2, written in mathematics as √2 or 21⁄2, is the positive irrational number that, when multiplied by itself, equals the number 2.[1] To be more correct, it is called the principal square root of 2, to tell it apart from the negative version of itself where that is also true.
Geometrically, the square root of 2 is the length of a diagonal across a square with sides with a length of one; this can be found with the Pythagorean theorem. Because of that, it is also called the Pythagoras's constant.[2]
Proof that the square root of 2 is not rational[change | change source]
The number is not rational. Here is the proof.[3]
- Assume that is rational. So there are some numbers such that .
- We can choose a and b so that either a or b is odd. If a and b were both even, then the fraction could be simplified (for example, instead of writing , we could write instead).
- If both sides of the equation are squared, then we get a2 / b2 = 2 and a2 = 2 b2.
- The right side is . This number is even. So the left side must be even too, which means that is even. If an odd number is squared, then an odd number will be the result. And if an even number is squared, an even number would be the result too. So is even.
- Because a is even, it can be written as: .
- The equation from the step 3 is used. We get 2b2 = (2k)2
- An exponentiation rule can be used (see the article) – the result is .
- Both sides are divided by 2. So . This means that is even.
- In step 2, we said that a is odd or b is odd. But in step 4, it was said that a is even, and in step 7, it was said that b is even. If the assumption we made in step 1 is true, then all these other things have to be true, but since they disagree with each other they can not all be true; that means that our assumption is not true.
Therefore, it is not true that is a rational number. So must be irrational.
Related pages[change | change source]
References[change | change source]
- ↑ "Compendium of Mathematical Symbols". Math Vault. 2020-03-01. Retrieved 2020-08-28.
- ↑ Weisstein, Eric W. "Pythagoras's Constant". mathworld.wolfram.com. Retrieved 2020-08-28.
- ↑ "Irrationality of the square root of 2". www.math.utah.edu. Retrieved 2020-08-28.












