Cauchy sequence

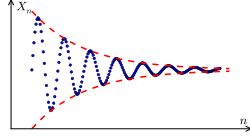
(a) The plot of a Cauchy sequence $(x_{n}),$ shown in blue, as $x_{n}$ versus $n$ If the space containing the sequence is complete, the "ultimate destination" of this sequence (that is, the limit) exists.

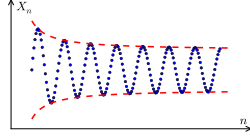
(b) A sequence that is not Cauchy. The elements of the sequence fail to get arbitrarily close to each other as the sequence progresses.

In mathematics, a Cauchy sequence is a sequence where the distance between any two elements of the sequence decreases as the sequence progresses. Cauchy sequences are named after Augustin-Louis Cauchy.