Dynamical systems theory
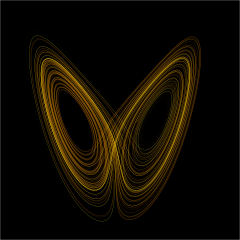
Dynamical systems theory is a field of applied mathematics that studies objects that change over time. Mathematicians in this field study equations that define these objects. A classic example includes equations of motion, which have been used to learn about basic behavior of mechanical systems. Equations can either describe changes across finite periods of time (or difference equations) or changes with time being continuous time (differential equations). When differential equations are used, the theory is called continuous dynamical systems theory. When difference equations are used, it is called discrete dynamical systems theory.
The theory looks at the long-term behaviour of dynamical systems. The study also includes the motion of planets, or electronic circuits.
