Kirchhoff's circuit laws
In 1845, German physicist Gustav Kirchhoff described two laws about electrical circuits.. These laws are generalizations of Ohm's law. Kirchhoff's circuit laws are very useful in solving circuit problems.
Kirchhoff's current law[change | change source]
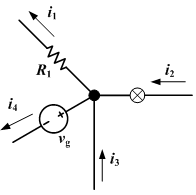
Kirchhoff's current law is also known as Kirchhoff's first law and Kirchhoff's junction law. This law states that 'The sum of current into a junction equals the sum of current out of the junction'. This is the same as Kirchhoff's junction law. In a junction, the electric charge's sum preservation law is applied. If the entering value of the current is i2 and i3, this current splits into the current of i1 and i4. Then the equation (i1 + i4 = i2 + i3) is satisfied. The right picture gives an example. This Kirchhoff's first law is that charge is not destroyed or created in a junction point. This is based by an electric charge preservation law.
Kirchhoff's voltage law[change | change source]
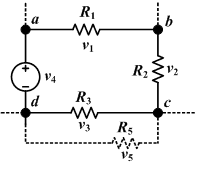
Kirchhoff's voltage law is also known as Kirchhoff's second law, a closed circuit law and Kirchhoff's loop law.
The algebraic sum of the voltage (potential) differences in any loop must equal zero.(This circuit is a closed circuit) Any complex circuit can be divided into many closed circuits. This law means that in the circuit there is an electric cell and electric resistance. The electric cell gives the charge a electromotive force, and then the electric resistance dissipates this force. But in electric resistance if the direction is opposite of the current's direction, this electric resistance adds to the electromotive force. This Kirchhoff's second law is based on potential energy preservation law.
