Surjective function

|
| Surjection. There is an arrow to every element in the codomain B from (at least) one element of the domain A. |
In mathematics, a surjective or onto function is a function f : A → B with the following property. For every element b in the codomain B, there is at least one element a in the domain A such that f(a)=b. This means that no element in the codomain is unmapped, and that the range and codomain of f are the same set.[1][2][3]
The term surjection and the related terms injection and bijection were introduced by the group of mathematicians that called itself Nicholas Bourbaki.[4] In the 1930s, this group of mathematicians published a series of books on modern advanced mathematics. The French prefix sur means above or onto and was chosen since a surjective function maps its domain on to its codomain.
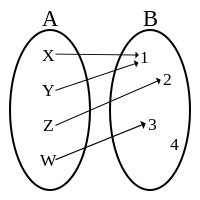
|
| Not a surjection. No element in the domain A is mapped to the element {4} in the codomain B. |
Basic properties[change | change source]
Formally:[5]
- is a surjective function if such that
where the element is called the image of the element , and the element a pre-image of the element .
The formal definition can also be interpreted in two ways:
- Every element of the codomain B is the image of at least one element in the domain A.
- Every element of the codomain B has at least one pre-image in the domain A.
A pre-image does not have to be unique. In the top image, both {X} and {Y} are pre-images of the element {1}. It is only important that there be at least one pre-image.
Examples[change | change source]
Elementary functions[change | change source]
Let f(x):ℝ→ℝ be a real-valued function y=f(x) of a real-valued argument x. (This means both the input and output are numbers.)
- Graphic meaning: The function f is a surjection if every horizontal line intersects the graph of f in at least one point.
- Analytic meaning: The function f is a surjection if for every real number yo we can find at least one real number xo such that yo=f(xo).
Finding a pre-image xo for a given yo is equivalent to either question:
- Does the equation f(x)-yo=0 have a solution? or
- Does the function f(x)-yo have a root?
In mathematics, we can find exact (analytic) roots only of polynomials of first, second (and third) degree. We find roots of all other functions approximately (numerically). This means a formal proof of surjectivity is rarely direct. So the discussions below are informal.
Example: The linear function of a slanted line is onto. That is, y=ax+b where a≠0 is a surjection. (It is also an injection and thus a bijection.)
- Proof: Substitute yo into the function and solve for x. Since a≠0 we get x= (yo-b)/a. This means xo=(yo-b)/a is a pre-image of yo. This proves that the function y=ax+b where a≠0 is a surjection. (Since there is exactly one pre-image, this function is also an injection.)
- Practical example: y= –2x+4. What is the pre-image of y=2? Solution: Here a= –2, i.e. a≠0 and the question is: For what x is y=2? We substitute y=2 into the function. We get x=1, i.e. y(1)=2. So the answer is: x=1 is the pre-image of y=2.
Example: The cubic polynomial (of third degree) f(x)=x3-3x is a surjection.
- Discussion: The cubic equation x3-3x-yo=0 has real coefficients (a3=1, a2=0, a1=–3, a0=–yo). Every such cubic equation has at least one real root.[6] Since the domain of the polynomial is ℝ, the means that ther is at least one pre-image xo in the domain. That is, (x0)3-3x0-yo=0. So the function is a surjection. (However, this function is not an injection. For example, yo=2 has 2 pre-images: x=–1 and x=2. In fact, every y, –2≤y≤2 has at least 2 pre-images.)
Example: The quadratic function f(x) = x2 is not a surjection. There is no x such that x2 = −1. The range of x² is [0,+∞) , that is, the set of non-negative numbers. (Also, this function is not an injection.)
Note: One can make a non-surjective function into a surjection by restricting its codomain to elements of its range. For example, the new function, fN(x):ℝ → [0,+∞) where fN(x) = x2 is a surjective function. (This is not the same as the restriction of a function which restricts the domain!)
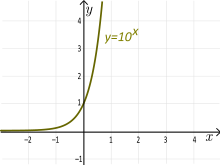
Example: The exponential function f(x) = 10x is not a surjection. The range of 10x is (0,+∞), that is, the set of positive numbers. (This function is an injection.)
Other examples with real-valued functions[change | change source]
Example: The logarithmic function base 10 f(x):(0,+∞)→ℝ defined by f(x)=log(x) or y=log10(x) is a surjection (and an injection). (This is the inverse function of 10x.)
- The projection of a Cartesian product A × B onto one of its factors is a surjection.
Example: The function f((x,y)):ℝ²→ℝ defined by z=y is a surjection. Its graph is a plane in 3-dimensional space. The pre-image of zo is the line y=zo in the x0y plane.
- In 3D games, 3-dimensional space is projected onto a 2-dimensional screen with a surjection.
Related pages[change | change source]
References[change | change source]
- ↑ "The Definitive Glossary of Higher Mathematical Jargon". Math Vault. 2019-08-01. Retrieved 2020-09-08.
- ↑ Weisstein, Eric W. "Surjection". mathworld.wolfram.com. Retrieved 2020-09-08.
- ↑ C.Clapham, J.Nicholson (2009). "Oxford Concise Dictionary of Mathematics, Onto Mapping" (PDF). Addison-Wesley. p. 568. Retrieved 2014-01-01.
- ↑ Miller, Jeff (2010). "Earliest Uses of Some of the Words of Mathematics". Tripod. Retrieved 2014-02-01.
- ↑ "4.3 Injections and Surjections". www.whitman.edu. Retrieved 2020-09-08.
- ↑ Tanton, James (2005). "Cubic equation". Encyclopedia of Mathematics. Facts on File, New York. p. 112-113. ISBN 0-8160-5124-0. (in English)
Other websites[change | change source]
- "Injective, Surjective, Bijective". 2013. Retrieved 2013-12-01. interactive quiz
- "Injectivity, Surjectivity". Wolfram alpha. Archived from the original on 2013-11-25. Retrieved 2013-12-01. interactive