Absolute value

The graph of the absolute value function for real numbers.

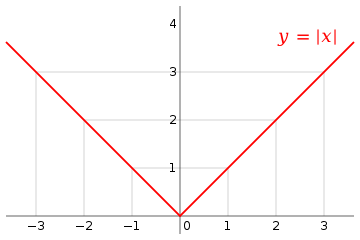
In mathematics, the absolute value of a real number is the number without the sign. The absolute value of 2 is 2, the absolute value of -2 is also 2. This notation is to express a numbers distance from zero on a number line. The absolute value of 10 would be 10 since the number 10 is 10 numbers away from zero, same follows with negatives.

$\begin{cases} \ \;\,\ \ x &\mathrm{if}\ x \ge 0\\ \ \;\, - x &\mathrm{otherwise} \end{cases}$

Properties

For any real number x the absolute value or modulus of x is denoted by | x | (a vertical bar on each side of the quantity) and is defined as

$|x| = \begin{cases} x, & \mbox{if } x \ge 0 \\ -x, & \mbox{if } x < 0. \end{cases}$

The absolute value of x is always either positive or zero, but never negative.

From an analytic geometry point of view, the absolute value of a real number is that number's distance from zero along the real number line. The absolute value of the difference of two real numbers is the distance between them.

The square-root notation without sign represents the positive square root. So, it follows that

$|a| = \sqrt{a^2}$

(1)

which is sometimes used as a definition of absolute value.

The absolute value has the following four main properties:

$|a| \ge 0$	(2)	Non-negativity
$|a| = 0 \iff a = 0$	(3)	Positive-definiteness
$|ab| = |a||b|\,$	(4)	Multiplicativeness
$|a+b| \le |a| + |b|$	(5)	Subadditivity

Other important properties of the absolute value include:

$||a|| = |a|\,$	(6)	Idempotence (the absolute value of the absolute value is the absolute value)
$|-a| = |a|\,$	(7)	Symmetry
$|a - b| = 0 \iff a = b$	(8)	Identity of indiscernibles (equivalent to positive-definiteness)
$|a - b| \le |a - c| +|c - b|$	(9)	Triangle inequality (equivalent to subadditivity)
$|a/b| = |a| / |b| \mbox{ (if } b \ne 0) \,$	(10)	Preservation of division (equivalent to multiplicativeness)
$|a-b| \ge ||a| - |b||$	(11)	(equivalent to subadditivity)

Two other useful properties concerning inequalities are:

$|a| \le b \iff -b \le a \le b$

$|a| \ge b \iff a \le -b \mbox{ or } b \le a$

These relations may be used to solve inequalities involving absolute values. For example:

$|x-3| \le 9$	$\iff -9 \le x-3 \le 9$
	$\iff -6 \le x \le 12$