Differential geometry
Differential geometry is a field of mathematics. It uses differential and integral calculus as well as linear algebra to study problems of geometry. The theory of the plane, as well as curves and surfaces in Euclidean space are the basis of this study. Big discoveries were made in the 18th and 19th century. In geometry, the sum of the angles of a triangle is 180 degrees. Carl Friedrich Gauß wondered whether triangle bearings of ships really has a sum of angles of exactly 180 degrees; with this question he was among the pioneers of modern differential geometry.
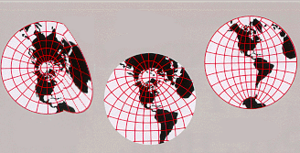
A long time ago, differential geometry was used for map projections. Today, it is used for fields as diverse as general relativity theory, or satellite navigation. Grigori Perelman's proof of the Poincaré conjecture uses differential geometry.
