Hypercube
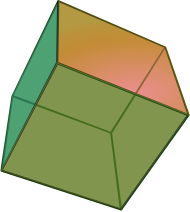
|

|
| Cube (3-cube) | Tesseract (4-cube) |
|---|
In geometry, a hypercube is an n-dimensional analogue of a square (n = 2) and a cube (n = 3). It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimension is equal to .
An n-dimensional hypercube is also called an n-cube or an n-dimensional cube. The term "measure polytope" is also used, notably in the work of H. S. M. Coxeter (originally from Elte, 1912),[1] but it has now been superseded.
The hypercube is the special case of a hyperrectangle (also called an n-orthotope).
A unit hypercube is a hypercube whose side has length one unit. Often, the hypercube whose corners (or vertices) are the 2n points in Rn with each coordinate equal to 0 or 1 is called "the" unit hypercube.
Construction[change | change source]


A hypercube can be defined by increasing the numbers of dimensions of a shape:
- 0 – A point is a hypercube of dimension zero.
- 1 – If one moves this point one unit length, it will sweep out a line segment, which is a unit hypercube of dimension one.
- 2 – If one moves this line segment its length in a perpendicular direction from itself; it sweeps out a 2-dimensional square.
- 3 – If one moves the square one unit length in the direction perpendicular to the plane it lies on, it will generate a 3-dimensional cube.
- 4 – If one moves the cube one unit length into the fourth dimension, it generates a 4-dimensional unit hypercube (a unit tesseract).
This can be generalized to any number of dimensions. This process of sweeping out volumes can be formalized mathematically as a Minkowski sum: the d-dimensional hypercube is the Minkowski sum of d mutually perpendicular unit-length line segments, and is therefore an example of a zonotope.
The 1-skeleton of a hypercube is a hypercube graph.
Related pages[change | change source]
- Simplex - the n-dimensional analogue of the triangle
- Hyperrectangle - the general case of the hypercube, where the base is a rectangle.
Notes[change | change source]
- ↑ Elte, E. L. (1912). "IV, Five dimensional semiregular polytope". The Semiregular Polytopes of the Hyperspaces. Netherlands: University of Groningen. ISBN 141817968X.
Other websites[change | change source]
- Eric W. Weisstein, Hypercube at MathWorld.
- Eric W. Weisstein, Hypercube graphs at MathWorld.
- Olshevsky, George, Measure polytope at Glossary for Hyperspace.
- www.4d-screen.de (Rotation of 4D – 7D-Cube)
- Rotating a Hypercube by Enrique Zeleny, Wolfram Demonstrations Project.
- Stereoscopic Animated Hypercube

