Law of large numbers
The law of large numbers, or LLN for short,[1] is a theorem from statistics. It states that if a random process is repeatedly observed, then the average of the observed values will be stable in the long run. This means that as the number of observations increases, the average of the observed values will get closer and closer to the expected value.
For example, when rolling dice, the numbers 1, 2, 3, 4, 5 and 6 are possible outcomes. They are all equally likely. The population mean (or "expected value") of the outcomes is:
- (1 + 2 + 3 + 4 + 5 + 6) / 6 = 3.5.
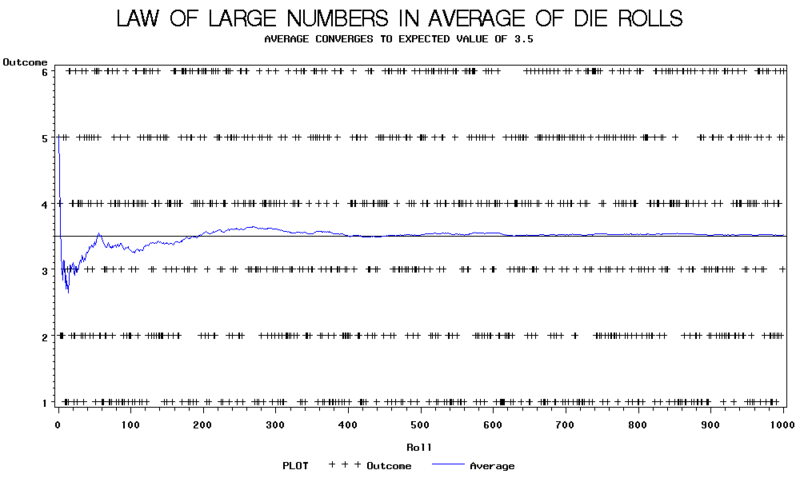
The following graph shows the results of an experiment of rolls of a die. In this experiment, it can be seen that the average of die rolls varies wildly at first, but as predicted by the LLN, the average stabilizes around the expected value of 3.5 as the number of observations become large.
History[change | change source]
Jacob Bernoulli first described the LLN. He says it was so simple that even the stupidest man instinctively knows it is true.[2] Despite this, it took him over 20 years to develop a good mathematical proof. Once he had found it, he published the proof in Ars Conjectandi (The Art of Conjecturing) in 1713. He named this his "golden theorem". It became generally known as "Bernoulli's theorem" (not to be confused with the law in physics with the same name). In 1835, S.D. Poisson further described it under the name "la loi des grands nombres" (the law of large numbers).[3] Thereafter, it was known under both names, but the "law of large numbers" is most frequently used.
Other mathematicians also contributed to make the law better. Some of them were Chebyshev (who proved a more general version of the law for averages[4]), Markov, Borel, Cantelli and Kolmogorov. After these studies, there are now two different forms of the law: One is called the "weak" law, and the other the "strong" law.[5] These forms do not describe different laws. They have different ways to describe the convergence of the observed or measured probability to the actual probability. The strong form of the law implies the weak one.
Related pages[change | change source]
References[change | change source]
- ↑ "List of Probability and Statistics Symbols". Math Vault. 2020-04-26. Retrieved 2020-10-14.
- ↑ Jakob Bernoulli, Ars Conjectandi: Usum & Applicationem Praecedentis Doctrinae in Civilibus, Moralibus & Oeconomicis, 1713, Chapter 4 (Translated into English by Oscar Sheynin)
- ↑ Hacking, Ian. (1983) "19th-century Cracks in the Concept of Determinism"
- ↑ "Law of large numbers | statistics". Encyclopedia Britannica. Retrieved 2020-10-14.
- ↑ "Law of Large Numbers". www.probabilitycourse.com. Retrieved 2020-10-14.