Trigonometry

Trigonometry (from the Greek trigonon = three angles and metro = measure) is a part of elementary mathematics dealing with angles, triangles and trigonometric functions such as sine (abbreviated sin), cosine (abbreviated cos) and tangent (abbreviated tan). It has some connection to geometry, although there is disagreement on exactly what that connection is; for some, trigonometry is just a section of geometry.

Overview and definitions in Trigonometry [change]

A standard right triangle. C is the right angle in this picture.

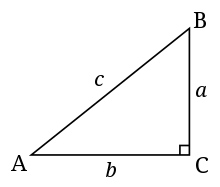
Trigonometry uses a large number of specific words to describe parts of a triangle. Some of the definitions in trigonometry are:

Right-angled triangle - A right-angled triangle is a triangle that has one angle that is equal to 90 degrees. (A triangle can not have more than one right angle.) The standard trigonometric ratios can only be used on right-angled triangles.
Hypotenuse - The hypotenuse of a triangle is the longest side, and the side that is opposite the right angle. For example, for the triangle on the right, the hypotenuse is side c.
Opposite of an angle - The opposite side of an angle is the side that does not intersect with the vertex of the angle. For example, side a is the opposite of angle A in the triangle to the right.
Adjacent of an angle - The adjacent side of an angle is the side that intersects the vertex of the angle but is not the hypotenuse. For example, side b is adjacent to angle A in the triangle to the right.

Trigonometric Ratios [change]

There are three main trigonometric ratios for right triangles, and three reciprocals of those ratios. There are 6 total ratios. They are:

Sine (sin) - The sine of an angle is equal to the ${Opposite \over Hypotenuse}$

Cosine (cos) - The cosine of an angle is equal to the ${Adjacent \over Hypotenuse}$

Tangent (tan) - The tangent of an angle is equal to the ${Opposite \over Adjacent}$

The reciprocals of these ratios are:

Cosecant (csc) - The cosecant of an angle is equal to the ${Hypotenuse \over Opposite}$ or $\csc \theta = {1 \over \sin \theta}$

Secant (sec) - The secant of an angle is equal to the ${Hypotenuse \over Adjacent}$ or $\sec \theta = {1 \over \cos \theta}$

Cotangent (cot) - The cotangent of an angle is equal to the ${Adjacent \over Opposite}$ or $\cot \theta = {1 \over \tan \theta}$

Students often use a mnemonic to remember this relationship. The sine, cosine, and tangent ratios in a right triangle can be remembered by representing them as strings of letters, such as SOH-CAH-TOA:

Sine = Opposite ÷ Hypotenuse

Cosine = Adjacent ÷ Hypotenuse

Tangent = Opposite ÷ Adjacent

or:

Some Old Horse Caught A Horse Taking Oats Away

or:

Some Officers Have Curly Auburn Hair Till Old Age

or:

Stephen Opens His Car And Hits The Open Avenue