Adiabatic process
An adiabatic process is a thermodynamic process where a fluid becomes warmer or cooler without getting heat from, or giving it to, something else. Usually the temperature instead changes because of changes in pressure.
Adiabatic cooling is the usual cause of clouds. When warm, humid air rises due to convection or other cause, water condenses to make clouds, and in some cases precipitation. Convection also causes cold air to sink. This warms it adiabatically, often destroying a cloud and sometimes causing any precipitation to evaporate before hitting the ground.
Description[change | change source]

If we take some fluids in an insulated system and expand or compress the system very fast, the system won't be able to gain or loose any heat (from outside of the system). (In reality, you can't get a perfectly insulated system. But in some cases, the heat transfer is so low that we can call them adiabatic process.)
From the first law of thermodynamics, we know that,[1]
Here, is the change of internal energy; is the change of heat and is the change of work.
Since there occurs no heat transfer in adiabatic process, the becomes 0. So, for adiabatic process, the equation is,
Again, we know that .(;; ; so, )
Here, is volume; is force; is pressure; is the area and is the distance.
So, the equation stands as,
Which means, by doing work (changing volume), one can change the internal energy (and so the temperature) in a adiabatic process.
Adiabatic process for ideal gas (for reversible adiabatic process)[change | change source]
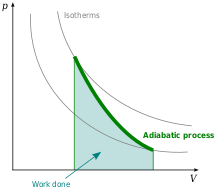
In the case of Adiabatic process (see the upper section),
Again, in constant volume, the heat capacity of one mole gas is,
Here, is the change of temperature and is the temperature।
But, in constant volume (as no work is done),
So,
From the first (1) equation,
Now, the Ideal gas law for one mole gas is,
Here, is the gas constant.
By differentiating the last equation,
Or,
Now from equation (2), we get,
Since, (Mayer's relation),
Here, is the heat capacity of gas at constant pressure.
Simplifying the equation (3),
If,
- ,
Then,
By dividing both sides of the equation (4) with we get,
Integrating (Integration leaves a constant) the equation (5),
If we assume that,
- ,
We get,
Simplifying the equation (6),
This is the relation between pressure and volume in adiabatic process.
References[change | change source]
- ↑ Franz, Mandl (8 January 1991). Statistical Physics (2nd ed.). John Wiley & sons. ISBN 978-0471915331.







































