Cross product
The English used in this article or section may not be easy for everybody to understand. (May 2020) |
The cross product is a mathematical operation which can be done between two three-dimensional vectors. It is often represented by the symbol .[1] After performing the cross product, a new vector is formed. The cross product of two vectors is always perpendicular (it makes a corner-shaped angle) to both of the vectors which were "crossed".[2][3] This means that cross product normally works only in three-dimensional space; that is, anywhere where you can go up or down, left or right, and forward or backwards.
Information about vectors[change | change source]
A vector is information that describes two things: which way (direction), and how much (magnitude). Usually, the simplest vector can be an arrow. How long is the line, and which way does the line and the pointed end of the arrow go?
Importance of the cross product[change | change source]
Being a vector operation, the cross product is extremely important in all sorts of sciences (particularly physics), engineering, and mathematics. One important example of the cross product involves torque (pushing or pulling in a circle, like twisting off a bottle cap.) or moment. Another important application involves the magnetic field.
Visualizing the cross product in three dimensions[change | change source]
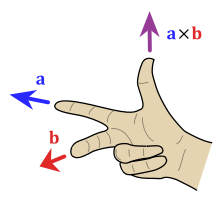
The cross product of and is a vector that we shall call :
The vector is perpendicular to both and . The direction of is determined by a variation of the right-hand rule. By holding your right hand as shown in the picture, your thumb points in the direction of (the cross product of and ), with the index finger pointing in the direction that points, and the middle finger pointing in the direction that points. If the angle between the index (your pointer finger) and middle (second finger away from your thumb) fingers is greater than 180°, then you need to turn the hand upside down.
How to calculate the cross product in vector notation[change | change source]
Like any mathematical operation, the cross product can be done in a straightforward way.
Two dimensions[change | change source]
Since cross products usually only work for three-dimensional vectors, the calculation of cross product in two dimensions thinks of the vectors as if they are on a flat surface (like a sheet of paper) in three dimensions (like a room or a large cube).
More specifically, if
and
then
or
and
where is just a symbol indicating that the new vector is pointing up (in the z-direction). If one "crosses" two vectors which are both in the xy-plane, then the product, being perpendicular to both vectors, must point in the z direction. If the value of is positive, then it points out of the page; if its value is negative, then it points into the page.
Three dimensions[change | change source]
There are two ways to find the cross product of two 3D vectors: with coordinate notation or with angle.
Coordinate notation[change | change source]
Given vectors and , where
and
Then the cross product of and is:
.[2]
With angle[change | change source]
Given vectors and , where
and
Then the cross product of and is:
,[2]
where is the angle between and , ‖a‖ and ‖b‖ are the magnitudes of vectors and , and n is a unit vector perpendicular to the plane containing and .
Basic properties of the cross product[change | change source]
Related pages[change | change source]
References[change | change source]
- ↑ "Comprehensive List of Algebra Symbols". Math Vault. 2020-03-25. Retrieved 2020-09-06.
- ↑ 2.0 2.1 2.2 2.3 2.4 Weisstein, Eric W. "Cross Product". mathworld.wolfram.com. Retrieved 2020-09-06.
- ↑ "Cross Product". www.mathsisfun.com. Retrieved 2020-09-06.





















