Mathematics

Math is the study of numbers, shapes, and patterns. The word comes from the Greek μάθημα (máthema), meaning "science, knowledge, or learning", and is sometimes shortened to math or maths.
It is the study of:
- Numbers: including how things can be counted.
- Structure: including how things are organized, but also how they can be or could have been. This subfield is usually called algebra.
- Place: where things are, and spatial arrangement, including arrangements of spaces themselves. This subfield is usually called geometry.
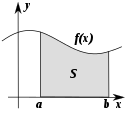
- Change: how things become different. This subfield is usually called analysis.
Applied math is useful for solving problems in the real world. People working in business, science, engineering, and construction use math.[1][2]
Problem-solving in math[change | change source]
Math solves problems by using logic. One of the main tools of logic used by mathematicians is deduction. Deduction is a special way of thinking to discover and prove new truths using old truths. To a mathematician, the reason something is true (called a proof) is just as important as the fact that it is true, and this reason is often found using deduction. Using deduction is what makes mathematical thinking different from other kinds of scientific thinking, which might rely on experiments or on interviews.[3]
Logic and reasoning are used by math people to create general rules, which are an important part of math. These rules leave out information that is not important so that a single rule can cover many situations. By finding general rules, mathematics solves many problems at the same time as these rules can be used on other problems.[4] These rules can be called theorems (if they have been proven) or conjectures (if it is not known if they are true yet).[5] Most math people use non-logical and creative reasoning in order to find a logical proof.[6]
Sometimes, math people finds and studies rules or ideas that we don't understand yet. Often in mathematics, ideas and rules are chosen because they are considered simple or neat. On the other hand, sometimes these ideas and rules are found in the real world after they are studied in mathematics; this has happened many times in the past. In general, studying the rules and ideas of mathematics can help us understand the world better. Some examples of math problems are addition, subtraction, multiplication, division, calculus, fractions and decimals. Algebra problems are solved by evaluating certain variables. A calculator answers every math problem in the four basic arithmetic operations.
Areas of study in math[change | change source]
Number[change | change source]
- Math includes the study of numbers and quantities. It is a branch of science that deals with the logic of shape, quantity, and arrangement. Most of the areas listed below are studied in many different fields of mathematics, including set theory and mathematical logic. The study of number theory usually focuses more on the structure and behavior of the integers rather than on the actual foundations of numbers themselves, and so is not listed in this given subsection.
Natural numbers Integers Rational numbers Real numbers Complex numbers Ordinal numbers Cardinal numbers Arithmetic operations Arithmetic relations Functions, see also special functions
Structure[change | change source]
- Structural math studies objects' and constructions' shape and integrity. These are areas of algebra and calculus.
Shape[change | change source]
- Some areas of math study the shapes of things. Most of these areas are part of the study of geometry.
Change[change | change source]
- Some areas of math study the way things change. Most of these areas are part of the study of analysis.
Applied mathematics[change | change source]
- Applied math uses symbolic logic to solve problems in areas like engineering and physics.
- Numerical analysis – Optimization – Probability theory – Statistics – Mathematical finance – Game theory – Mathematical physics – Fluid dynamics - Computational algorithms
Famous theorems[change | change source]
These theorems and conjectures have interested mathematicians and amateurs alike:
- Pythagorean theorem – FLT – Goldbach's conjecture – Twin Prime Conjecture – Gödel's incompleteness theorems – Poincaré conjecture – Cantor's diagonal argument – Four color theorem – Zorn's lemma – Euler's Identity – Church-Turing thesis
These theorems and hypotheses have greatly changed mathematics:
- Central limit theorem classification theorems of surfaces – Continuum hypothesis – Fourier Theorem – Fundamental theorem of calculus – Fundamental theorem of algebra – Fundamental theorem of arithmetic – Fundamental theorem of projective geometry – Gauss-Bonnet theorem - Kantorovich theorem – P Versus NP – Pythagorean theorem – Riemann hypothesis
These are a few conjectures that have been called "revolutionary":
- Beal Conjecture (a generalization of FLT) – Birch and Swinnerton-Dyer Conjecture – Collatz Conjecture – Goldbach's Conjecture –Hodge Conjecture – Poincaré Conjecture
Foundations and methods[change | change source]
- Set theory – Symbolic logic – Model theory – Category theory – Logic – Table of mathematical symbols
History and the world of mathematicians[change | change source]
- History of mathematics – Timeline of mathematics – Mathematicians – Fields Medal – Abel Prize – Millennium Prize Problems (Clay Math Prize) – International Mathematical Union – Mathematics competitions – Lateral thinking – Mathematics and gender
Awards in mathematics[change | change source]
There is no Nobel Prize in mathematics. Mathematicians can receive the Abel Prize and the Fields Medal for important works.[7][8]
The Clay Mathematics Institute has said it will give one million dollars to anyone who solves one of the Millennium Prize Problems.
Mathematical tools[change | change source]
There are many tools used to do math or find answers to math problems.
- Older tools
- Newer tools
- Graphing calculators, scientific calculators and more complex computer visual tools
- Programming languages
- Computer algebra systems (listing) and automated matrix analysis
- statistics software (for example SPSS)
- SAS (programming language)
- R (programming language)
References[change | change source]
- ↑ "Thinking of a Career in Applied Mathematics? | SIAM". www.siam.org. Retrieved 2018-07-30.
- ↑ Wigner, Eugene (February 1960). "The Unreasonable Effectiveness of Mathematics in the Natural Sciences". Communications in Pure and Applied Mathematics. 13 (1): 1–14. Bibcode:1960CPAM...13....1W. doi:10.1002/cpa.3160130102. S2CID 6112252. Archived from the original on 2018-08-10. Retrieved 2018-08-07.
- ↑ "The science checklist applied: Mathematics". undsci.berkeley.edu. Retrieved 2018-08-05.
- ↑ "The Role of Generalization in the Advanced Mathematical Thinking". AMS Grad Blog. 2016-08-21. Retrieved 2018-08-07.
- ↑ Houston, Kevin (2009). How to Think Like a Mathematician. Cambridge University Press. p. 99. ISBN 978-0-521-71978-0.
- ↑ Thurston, William (April 1994). "On proof and progress in mathematics". Bulletin of the American Mathematical Society. 30 (2): 161–177. arXiv:math/9404236. Bibcode:1994math......4236T. doi:10.1090/S0273-0979-1994-00502-6.
- ↑ Ronan, Mark (2014-08-13). "The Fields Medal is the greatest prize in maths [sic]". The Daily Telegraph. ISSN 0307-1235. Retrieved 2018-08-07.
- ↑ Bellos, Alex (2018-03-20). "Abel Prize 2018: Robert Langlands wins for 'unified theory of maths' [sic]". the Guardian. Retrieved 2018-08-07.
Related pages[change | change source]
- Timeline of women in mathematics
- American Mathematical Society
- Society for Industrial and Applied Mathematics
- International Congress on Industrial and Applied Mathematics
- International Congress of Mathematicians
- International Mathematical Olympiad
- Mathematics Genealogy Project
- Mathematics Subject Classification
Other websites[change | change source]
- Mathematics Citizendium
- Mathematics at the Open Directory Project