Probability density function
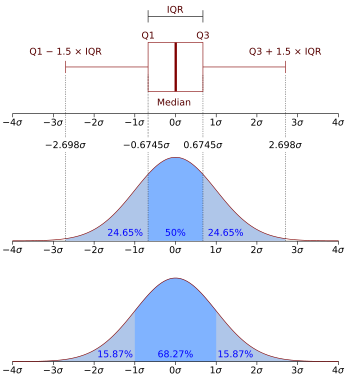
In probability and statistics, a probability density function is a function that characterizes any continuous probability distribution. For a random variable X, the probability density function of X is sometimes written as .[1] The integral of the probability density function in the interval yields the probability that a given random variable with the given density is contained in the interval provided.[2] By definition, the probability density function is non-negative throughout its domain, on which the integral sums up to 1.[3]
Probability density versus probability mass function[change | change source]
The probability mass function is to a discrete probability distribution what the probability density function is to a continuous probability distribution. The probability density function is necessary to be able to work with continuous distributions.
A random variable with a continuous probability distribution can take on any value within that distribution. Casting a dice will give the numbers 1 to 6, with a probability of , but this is not a continuous function, as only the numbers 1 to 6 are possible.
In contrast, two people will not have the same height or the same weight. Using a probability density function, it is possible to determine the probability for people between 180 centimetres (71 in) and 181 centimetres (71 in), or between 80 kilograms (176.4 lb) and 81 kilograms (178.6 lb), even though there are infinitely many values between these two bounds.
References[change | change source]
- ↑ "List of Probability and Statistics Symbols". Math Vault. 2020-04-26. Retrieved 2020-09-13.
- ↑ Weisstein, Eric W. "Probability Density Function". mathworld.wolfram.com. Retrieved 2020-09-13.
- ↑ Nykamp, Duane. "The idea of a probability density function". Math Insight. Retrieved September 13, 2020.


![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
