Chi-square distribution

chi-square
	Probability density function;
	Cumulative distribution function;
Parameters	degrees of freedom
Support
Probability density function (pdf)
Cumulative distribution function (cdf)
Mean
Median	approximately
Mode	if
Variance
Skewness
Excess kurtosis
Entropy
Moment-generating function (mgf)	for
Characteristic function

From Wikipedia, the free encyclopedia

Jump to: navigation, search

For other uses, see Chi.

In probability theory and statistics, the chi-square distribution (also chi-squared or $χ 2$ distribution) is one of the most widely used theoretical probability distributions. It is used in statistical significance tests. It is useful, because it is relatively easy to show that certain probability distributions come close to it, under certain conditions. One of these conditions is that the null hypothesis must be true. Another one is that the different random variables (or observations) must be independent of each other.

This short article can be made longer. You can help Wikipedia by adding to it.

Chi-square distribution

From Wikipedia, the free encyclopedia

Views

Personal tools

Search

Getting around

Print/export

Toolbox

In other languages

Probability density function
Cumulative distribution function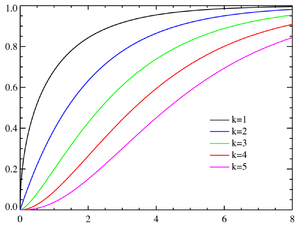
Parameters	$k > 0\,$ degrees of freedom
Support	$x \in [0; +\infty)\,$
Probability density function (pdf)	$\frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}\,$
Cumulative distribution function (cdf)	$\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}\,$
Mean	$k\,$
Median	approximately $k-2/3\,$
Mode	$k-2\,$ if $k\geq 2\,$
Variance	$2\,k\,$
Skewness	$\sqrt{8/k}\,$
Excess kurtosis	$12/k\,$
Entropy	$\frac{k}{2}\!+\!\ln(2\Gamma(k/2))\!+\!(1\!-\!k/2)\psi(k/2)$
Moment-generating function (mgf)	$(1-2\,t)^{-k/2}$ for $2\,t<1\,$
Characteristic function	$(1-2\,i\,t)^{-k/2}\,$