Condorcet method

A Condorcet method (English: /kɒndɔːrˈseɪ/; French: [kɔ̃dɔʁsɛ]) is one of many election methods that elects the candidate that is preferred by more voters than their opponent in every head-to-head election against each of the other candidates, whenever there is such a candidate. This candidate, known as the pairwise champion or beats-all winner, is formally called the Condorcet winner.
A Condorcet winner might not always exist in a particular election because the preference of a group of voters selecting from more than two options can possibly be cyclic — that is, it is possible (but very rare) that every candidate has an opponent that defeats them in a two-candidate contest. (This is similar to the game rock paper scissors, where each hand shape wins against only one opponent and loses to another). The possibility of such cyclic preferences in a group of voters is known as the Condorcet paradox. However, there always exists a smallest group of candidates that beats all candidates not in the group, known as the Smith set, which is guaranteed to only have the Condorcet winner in it when one exists; many Condorcet methods always elect a candidate who is in the Smith set when there is no Condorcet winner, and are thus said to be "Smith-efficient". The Condorcet winner is also usually but not necessarily the utilitarian winner (the one which maximizes social welfare).[1][2]
Condorcet voting methods are named for the 18th-century French mathematician and philosopher Marie Jean Antoine Nicolas Caritat, the Marquis de Condorcet, who championed such voting systems. However, Ramon Llull devised the earliest known Condorcet method in 1299.[3] It always elects the same candidate as Copeland's method in cases with no pairwise ties.[4]
Condorcet methods usually use preferential (ranked) voting, though they can be done with separate rounds of runoff elections.
Most Condorcet methods have a single round of preferential voting, in which each voter ranks the candidates from most preferred (marked as number 1) to least preferred (marked with a higher number). A voter's ranking is often called their order of preference. The votes can be tallied in many ways to find a winner. Some - the Condorcet methods - will elect the Condorcet winner if there is one. They can also elect a winner when there is no Condorcet winner, and different Condorcet-compliant methods may elect different winners in the case of a cycle.
The procedure given in Robert's Rules of Order for voting on motions and amendments is also a Condorcet method, even though the voters do not vote by ranking the candidates. There are multiple rounds of voting, and in each round the vote is between two of the alternatives. The loser (by majority rule) of a pairing is eliminated, and the winner of a pairing is paired in a later round against another alternative. Eventually only one alternative remains, and it is the winner. This is similar to a single-winner or round-robin tournament; the total number of pairings is one less than the number of alternatives. Since a Condorcet winner will win by majority rule in each of its pairings, it will never be eliminated by Robert's Rules. But this method cannot reveal a voting paradox in which there is no Condorcet winner and a majority prefer an early loser over the eventual winner (though it will always elect someone in the Smith set). A lot of the literature on social choice theory is about this method since it is widely used and is used by important organizations (legislatures, councils, committees, etc.). It is not practical for use in public elections, however, since its multiple rounds of voting would be very expensive for voters, for candidates, and for governments.
Summary[change | change source]
In a competition between candidates A and B where voters have ranked the candidates, if more voters mark their ballots that they prefer candidate A over candidate B than the number of voters who mark their ballots to the contrary, then Candidate B is not (supposed to be) elected.
However, because of the possibility of the Condorcet paradox, it is possible, but unlikely,[5] that this can't be done. This is sometimes called a Condorcet cycle or just cycle and can be thought of as Candidate Rock beating Candidate Scissors, Candidate Scissors beating Candidate Paper, and Candidate Paper beating Candidate Rock. If there is no cycle (and no ties), all Condorcet methods elect the same candidate.
- Each voter ranks the candidates in order of preference (top-to-bottom, or best-to-worst, or 1st, 2nd, 3rd, etc.). The voter may be allowed to rank candidates as equals, to express indifference (no preference) between them. To save time, candidates omitted by a voter may be treated as if the voter ranked them at the bottom.[source?]
- For each pairing of candidates (as in a round-robin tournament) count how many votes rank each candidate over the other candidate. Thus each pairing will have two totals: the size of its majority and the size of its minority[source?] (or there will be a tie).
For most Condorcet methods, the pairwise counts are all that is necessary to figure out who won, who came in 2nd place, etc. and can be used to figure out if there is a Condorcet winner, and who it is.
Definition[change | change source]
A Condorcet method is a voting system that will always elect the Condorcet winner (if there is one); this is the candidate whom more voters prefer to each other candidate, when compared to them one at a time. This candidate can be found by checking if there is a candidate who beats all other candidates; this can be done by using Copeland's method and then checking if the Copeland winner has the highest possible Copeland score.
Note that there are ½N(N−1) pairwise comparisons for N candidates. For 10 candidates, this means there are 0.5*10*9=45 comparisons, which can make elections with many candidates hard to count the votes for.
In some situations, an election has no Condorcet winner. This occurs as a result of a kind of tie known as a majority rule cycle, described by Condorcet's paradox. Different Condorcet methods pick different winners in these situations. Some Condorcet methods involve the basic procedure described below, coupled with a Condorcet completion method, which is used to find a winner when there is no Condorcet winner. Other Condorcet methods involve an entirely different system of counting, but are classified as Condorcet methods because they will still elect the Condorcet winner if there is one.[source?]
It is important to note that not all single winner, ranked voting systems are Condorcet methods. For example, instant-runoff voting and the Borda count are not Condorcet methods.[source?]
Basic procedure[change | change source]
Finding the winner[change | change source]
In any Condorcet method that passes Independence of Smith-dominated alternatives, it can sometimes help to identify the Smith set from the head-to-head matchups, and eliminate all candidates not in the set before doing the procedure for that Condorcet method.
Condorcet methods use pairwise counting. For each possible pair of candidates, one pairwise count indicates how many voters prefer one of the paired candidates over the other candidate, and another pairwise count indicates how many voters have the opposite preference. The counts for all possible pairs of candidates show all the pairwise preferences of all the voters.
Pairwise counts are often displayed in a pairwise comparison matrix[6] or outranking matrix[7] such as those below. In these matrices, each row represents each candidate as a 'runner', while each column represents each candidate as an 'opponent'. The cells at the intersection of rows and columns each show the result of a particular pairwise comparison. Cells comparing a candidate to themselves are left blank.[8][9]
Imagine there is an election between four candidates: A, B, C and D. The first matrix below records the preferences expressed on a single ballot paper, in which the voter's preferences are (B, C, A, D); that is, the voter ranked B first, C second, A third, and D fourth. In the matrix a '1' indicates that the runner is preferred on this voter's ballot over the 'opponent', while a '0' indicates that the runner is defeated.[6][8] For example, in the following matrix, A beats D:
| A | B | C | D | ||
|---|---|---|---|---|---|
| A | — | 0 | 0 | 1 | |
| B | 1 | — | 1 | 1 | |
| C | 1 | 0 | — | 1 | |
| D | 0 | 0 | 0 | — | |
| A '1' indicates that the runner is preferred over the opponent; a '0' indicates that the runner is defeated. | |||||
Using a matrix like the one above, one can find the overall results of an election. Each ballot can be transformed into this style of matrix, and then added to all other ballot matrices using matrix addition. The sum of all ballots in an election is called the sum matrix.
Suppose that in the imaginary election there are two other voters. Their preferences are (D, A, C, B) and (A, C, B, D). Added to the first voter, these ballots would give the following sum matrix:
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 2 | 2 | 2 |
| B | 1 | — | 1 | 2 |
| C | 1 | 2 | — | 2 |
| D | 1 | 1 | 1 | — |
When the sum matrix is found, the contest between each pair of candidates is considered. The number of votes for runner over opponent (runner,opponent) is compared with the number of votes for opponent over runner (opponent,runner) to find the Condorcet winner. In the sum matrix above, A is the Condorcet winner because A beats every other candidate. When there is no Condorcet winner, many Condorcet completion methods, such as Ranked Pairs and the Schulze method, use the information contained in the sum matrix to choose a winner.
Cells marked '—' in the matrices above have a numerical value of '0', but a dash is used since candidates are never preferred to themselves. The first matrix, that represents a single ballot, is inversely symmetric: (runner,opponent) is ¬(opponent,runner). Or (runner,opponent) + (opponent,runner) = 1. The sum matrix has this property: (runner,opponent) + (opponent,runner) = N for N voters, if all runners were fully ranked by each voter.
Example: Voting on the location of Tennessee's capital[change | change source]
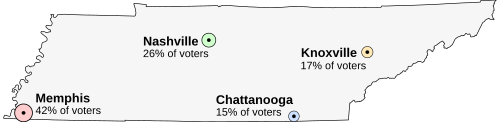
Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities and that everyone wants to live as near to the capital as possible.
The candidates for the capital are:
- Memphis, the state's largest city, with 42% of the voters, but located far from the other cities
- Nashville, with 26% of the voters, near the center of the state
- Knoxville, with 17% of the voters
- Chattanooga, with 15% of the voters
The preferences of the voters would be divided like this:
| 42% of voters (close to Memphis) |
26% of voters (close to Nashville) |
15% of voters (close to Chattanooga) |
17% of voters (close to Knoxville) |
|---|---|---|---|
|
|
|
|
To find the Condorcet winner every candidate must be matched against every other candidate in a series of one-on-one contests. In each pairing the winner is the candidate preferred by a majority of voters. The results for every possible pairing are as follows:
| Pair | Winner |
|---|---|
| Memphis (42%) vs. Nashville (58%) | Nashville |
| Memphis (42%) vs. Chattanooga (58%) | Chattanooga |
| Memphis (42%) vs. Knoxville (58%) | Knoxville |
| Nashville (68%) vs. Chattanooga (32%) | Nashville |
| Nashville (68%) vs. Knoxville (32%) | Nashville |
| Chattanooga (83%) vs. Knoxville (17%) | Chattanooga |
The results can also be shown in the form of a matrix:
| 1st | Nashville [N] | 3 Wins ↓ | |||
|---|---|---|---|---|---|
| 2nd | Chattanooga [C] | 1 Loss →
↓ 2 Wins |
[N] 68% [C] 32% | ||
| 3rd | Knoxville [K] | 2 Losses →
↓ 1 Win |
[C] 83% [K] 17% |
[N] 68% [K] 32% | |
| 4th | Memphis [M] | 3 Losses → | [K] 58% [M] 42% |
[C] 58% [M] 42% |
[N] 58% [M] 42% |
As can be seen from both of the tables above, Nashville beats every other candidate. This means that Nashville is the Condorcet winner. So Nashville would win an election held under any Condorcet method.
While any Condorcet method will elect Nashville as the winner, first-past-the-post and instant-runoff voting would select Memphis and Knoxville respectively, using the same ballots. This would occur despite the fact that most people would have preferred Nashville to either of those options. Condorcet methods make these preferences obvious rather than ignoring or discarding them.
On the other hand, note that in this example Chattanooga also defeats Knoxville and Memphis when paired against those cities. If Memphis voters had preferred Chattanooga as a second choice rather than as a third choice, then Chattanooga would be the Condorcet winner even though finishing in last place in a first-past-the-post election.
An alternative way of thinking about this example if a Smith-efficient Condorcet method that passes ISDA is used to determine the winner is that 58% of the voters, a mutual majority, ranked Memphis last (making Memphis the majority loser and Nashville, Chattanooga, and Knoxville above Memphis, ruling Memphis out. At that point, the voters who preferred Memphis as their 1st choice could only help to choose a winner among Nashville, Chattanooga, and Knoxville, and because they all preferred Nashville as their 1st choice among those three, Nashville would've had a 68% majority of 1st choices among the remaining candidates and won as the majority's 1st choice.
Two-method systems[change | change source]
Some Condorcet methods first do a series of pairwise comparisons and then, if there is no Condorcet winner, use an entirely different, non-Condorcet method to determine a winner. The simplest such fall-back methods completely ignore the results of the pairwise comparisons. For example, the Black method chooses the Condorcet winner if it exists, but uses the Borda count instead if there is a cycle (the method is named for Duncan Black).
A more complex two-stage process is, when there is a cycle, to first eliminate all candidates not in some group which is found by looking at the pairwise comparisons, and then use a separate voting system to find the winner. Sets used for this purpose are defined so that they will always contain only the Condorcet winner if there is one, and will always, in any case, contain at least one candidate. Such sets include the
- Smith set: The smallest non-empty set of candidates in a particular election such that every candidate in the set can beat all candidates outside the set. It is easily shown that there is only one possible Smith set for each election.
- Schwartz set: This is the innermost unbeaten set, and is usually the same as the Smith set. It is defined as the union of all possible sets of candidates such that for every set:
- Every candidate inside the set is pairwise unbeatable by any other candidate outside the set (i.e., ties are allowed).
- No proper (smaller) subset of the set fulfills the first property.
- Landau set (or uncovered set or Fishburn set): the set of candidates, such that each member, for every other candidate (including those inside the set), either beats this candidate or beats a third candidate that itself beats the candidate that is unbeaten by the member.
Single-method systems[change | change source]
Some Condorcet methods use a single procedure that meets the Condorcet criteria and, without any extra procedure, also pick winners when there are cycles. In other words, these methods do not involve separate procedures for different situations. Typically these methods base their calculations on pairwise counts. These methods include:
- Copeland's method: This simple method involves electing the candidate who wins the most pairwise matchings. However, it often produces a tie.
- Kemeny–Young method: This method ranks all the choices from most popular and second-most popular down to least popular.
- Minimax: Also called Simpson, Simpson–Kramer, and Simple Condorcet, this method chooses the candidate whose worst pairwise defeat is better than that of all other candidates. A possible improved modification to this method involves only allowing it to choose a winner from the Smith set; this has been called Smith/Minimax.
- Nanson's method and Baldwin's method combine the Borda Count with an instant runoff procedure.
- Dodgson's method extends the Condorcet method by swapping candidates until a Condorcet winner is found. The winner is the candidate which requires the minimum number of swaps.
- Ranked pairs breaks each cycle in the pairwise preference graph by dropping the weakest majority in the cycle, thereby yielding a complete ranking of the candidates. This method is also known as Tideman, after its inventor Nicolaus Tideman.
- Schulze method repeatedly drops the weakest majority in the pairwise preference graph until there is a Condorcet winner (unless there are ties). This method is also known as Schwartz sequential dropping (SSD), cloneproof Schwartz sequential dropping (CSSD), beatpath method, beatpath winner, path voting and path winner.
Related terms[change | change source]
- Other terms related to the Condorcet method are:
- Condorcet loser
- the candidate who is less preferred than every other candidate in a pairwise matchup (preferred by fewer voters than any other candidate).
- Weak Condorcet winner
- a candidate who beats or ties with every other candidate in a pairwise matchup (preferred by at least as many voters as any other candidate). There can be more than one weak Condorcet winner.
- Weak Condorcet loser
- a candidate who is defeated by or ties with every other candidate in a pairwise matchup. Similarly, there can be more than one weak Condorcet loser.
Condorcet ranking methods[change | change source]
Some Condorcet methods produce not just a single winner, but a ranking of all candidates from first to last place. A Condorcet ranking is a list of candidates with the property that the Condorcet winner (if one exists) comes first and the Condorcet loser (if one exists) comes last, and the same holds for the candidates ranked between them.
Methods that satisfy this property include:
- Copeland's method, Kemeny–Young method, Ranked pairs, Schulze method
Though there won't always be a Condorcet winner or Condorcet loser, there is always a Smith set and "Smith loser set" (smallest group of candidates who lose to all candidates not in the set in head-to-head elections). Some voting methods produce rankings that sort all candidates in the Smith set above all others, and all candidates in the Smith loser set below all others, with this also applying to all candidates ranked between them. Because the Smith set and Smith loser set are equivalent to the Condorcet winner and Condorcet loser when they exist, methods that always produce Smith set rankings also always produce Condorcet rankings.
Comparison with instant runoff and first-past-the-post (plurality)[change | change source]
Many proponents of instant-runoff voting (IRV) are attracted by the belief that if their first choice does not win, their vote will be given to their second choice; if their second choice does not win, their vote will be given to their third choice, etc. This sounds perfect, but it is not true for every voter with IRV. If someone voted for a strong candidate, and their 2nd and 3rd choices are eliminated before their first choice is eliminated, IRV gives their vote to their 4th choice candidate, not their 2nd choice. Condorcet voting takes all rankings into account simultaneously, but this makes it fail the later-no-harm criterion and the later-no-help criterion. With IRV, indicating a second choice will never hurt your first choice. With Condorcet voting, it is possible that indicating a second choice will cause your first choice to lose.
Plurality voting is simple, and theoretically provides incentives for voters to compromise for centrist candidates rather than throw away their votes on candidates who can't win. Opponents to plurality voting point out that voters often vote for the lesser of evils because they heard on the news that those two are the only two with a chance of winning, not necessarily because those two are the two good compromise candidates. This gives the media significant election powers. Condorcet runs each candidate against the other head to head, so that voters elect the candidate who would win the most sincere runoffs, instead of the one they thought they had to vote for.
There are circumstances, as in the examples above, when both instant-runoff voting and the 'first-past-the-post' plurality system wouldn't elect the Condorcet winner. (In fact, FPTP can elect the Condorcet loser and IRV can elect the second-worst candidate, who would lose to every candidate except the Condorcet loser.[10]) When there is a Condorcet winner that IRV doesn't elect, a majority would by definition prefer the Condorcet Winner to the IRV winner. Supporters of the Condorcet criterion see it as an important criterion when choosing a voting method. They see the Condorcet criterion as a natural extension of majority rule. Condorcet methods tend to encourage the selection of broadly supported candidates who appeal to the median voter. Here is an example that is designed to support IRV while making Condorcet look bad:
499 A>B>C
3 B>C>A
498 C>B>A
B is preferred by a 501–499 majority to A, and by a 502–498 majority to C. So, according to the Condorcet criterion, B should win, despite the fact that very few voters rank B in first place. By contrast, IRV elects C and plurality elects A. The goal of a ranked voting system is for voters to be able to vote sincerely and trust the system to protect their intent.
The importance of this scenario, of two parties with strong support, and the one with weak support being the Condorcet winner, may be less than one would expect, though, as it is common in plurality voting systems (see Duverger's law), but much less likely to occur in Condorcet or IRV elections, which unlike Plurality voting, punish candidates who are opposed by a significant block of voters.
Here is an example that is designed to support Condorcet while making IRV look bad:
33 A>B>C
16 B>A>C
16 B>C>A
35 C>B>A
B would win against either A or C by more than a 65–35 margin in a one-on-one election, but IRV eliminates B first, leaving a contest between the more "polar" candidates, A and C. Proponents of plurality voting state that their system is simpler than any other and more easily understood.
All three systems are susceptible to tactical voting, but the types of strategy used and how often there is value in voting strategically differ in each method.
Potential for tactical voting[change | change source]
Like all voting methods, Condorcet methods are vulnerable to compromising. That is, voters can help avoid the election of a less-preferred candidate by insincerely (strategically) raising the position of a more-preferred candidate on their ballot. However, Condorcet methods are only vulnerable to compromising when there is a majority rule cycle, or when one can be created.
All Condorcet methods are at least somewhat vulnerable to burying. That is, voters can sometimes help a more-preferred candidate by strategically lowering the ranking of a less-preferred candidate on their ballot.
Evaluation by criteria[change | change source]
Scholars of electoral systems often compare them using mathematically defined voting system criteria. The criteria which Condorcet methods satisfy vary from one Condorcet method to another. However, the Condorcet criterion implies the majority criterion, and thus is incompatible with independence of irrelevant alternatives (though it implies a weaker analagous form of the criterion: when there is a Condorcet winner, losing candidates can drop out of the election without changing the result), later-no-harm, the participation criterion, and the consistency criterion.
Use of Condorcet voting[change | change source]

Condorcet methods are not known to be currently in use in government elections anywhere in the world, but a Condorcet method known as Nanson's method was used in city elections in the U.S. town of Marquette, Michigan in the 1920s,[11] and today Condorcet methods are used by a number of private organizations. Organizations which currently use some variant of the Condorcet method are:
- The Wikimedia Foundation used the Schulze method to elect its Board of Trustees until 2013, when it switched to a ratings ballot with Support/Neutral/Oppose ballots.[12]
- The Pirate Party of Sweden uses the Schulze method for its primaries
- The Debian project uses the Schulze method for internal referendums and to elect its leader
- The Software in the Public Interest corporation uses the Schulze method for internal referendums and to elect its Board of Directors
- The Gentoo Foundation uses the Schulze method for internal referendums and to elect its Board of Trustees and its Council
- The Free State Project used Minimax for choosing its target state
- The uk.* hierarchy of Usenet
- The Student Society of the University of British Columbia uses ranked pairs for its executive elections.
- Kingman Hall and Hillegass Parker House, two loosely affiliated student housing cooperatives, each use the Schulze method to elect their management teams.
Other considerations[change | change source]
- If every seat in a legislature is elected (in separate elections, by the same pool of voters – use of districts will avoid this) by the Condorcet method, the legislators would all be centrists and might all agree with each on what laws to pass. Some voters prefer to have opposites in the legislature so they can't pass laws easily. These voters might prefer the Condorcet method for electing executive offices.
- If 10 candidates run for governor in a Condorcet race, ballot counters may need to count 9+8+7+6+5+4+3+2+1 = 45 head to head runoffs to find the winner. While this is doable, it might be more practical to still use ballot access laws or primaries, defeating some of the original intent of the Condorcet method. Possible solutions:
- Computers can be used to speed up the counts, though some voters fear computers can be hacked and used for ballot counting fraud.
- Another option would be to allow several independent scanner owners count the ballots and compare results. Volunteer hand counters could then spot check various candidates and ranks to make sure they match the subtotals reported by the scanners.
- It is also possible to limit the number of ranks voters can use; for example, if every voter is only allowed to rank each candidate either 1st, 2nd, or 3rd, with equal rankings allowed, then only the runoffs between candidates ranked 1st and 2nd, 1st and 3rd, 1st and last, 2nd and 3rd, 2nd and last, and 3rd and last need be counted, as the runoffs between two candidates at the same rank will result in ties.
- The negative vote-counting approach to pairwise counting may reduce the amount of work the vote-counters have to do. For example, with 10 candidates, a voter who ranks candidate A as their 1st choice and doesn't rank any other candidate prefers A over 9 other candidates. In the regular approach, this means recording those 9 preferences; but with negative counting, it can simply be recorded that A is marked on 1 voter's ballot, with this itself indicating that A is preferred in every match-up. When a voter ranks a candidate 2nd, then a negative vote can be placed in the matchup between the 2nd choice and 1st choice to indicate that the 2nd choice is not preferred to the 1st choice, such that it will cancel out with the support the 2nd choice would receive against the 1st choice from being marked on the voter's ballot. Negative votes can likewise be applied to matchups where both candidates are ranked equally.
- If there are no more than 5 candidates ( or a larger number of candidates is short-listed to 5) then the amount of effort counting ballots could be reduced to normal acceptable levels by asking voters to select an order of preference from a predetermined list of the possibilities. This would mean that the ballots would just require to be counted once to determine the number of votes cast for each order of preference. The results would then be entered into a simple spreadsheet which would determine the Condorcet winner. For example where there are candidates A, B and C, there are six orders of preference, so voters could be asked to choose which of the six they wish to vote for. Counting would then be simply a matter of counting how votes were cast for each order of preference. The results could then be applied to a simple spreadsheet which revealed the Condorcet winner. If there were four candidates (options) then there would be 24 orders of preference; if there were five candidates then there would be 120 orders of preference and so on.
- Voters make an economic trade-off in the amount of time invested in researching and ranking candidates. If voters rank too few candidates or rank such as to inaccurately represent their preferences, the Condorcet candidate cannot be correctly discovered. Nominating primaries reduce the number of candidates to avoid this, and the style of nominating primary can impact whether the Condorcet candidate—or at least a similar candidate—remains or if all such candidates are eliminated in favor of polarized options.
Related pages[change | change source]
- Condorcet loser criterion
- Ramon Llull (1232–1315) who, with the 2001 discovery of his lost manuscripts Ars notandi, Ars eleccionis, and Alia ars eleccionis, was given credit for discovering the Borda count and Condorcet criterion (Llull winner) in the 13th century
Notes and references[change | change source]
- ↑ Pivato, Marcus (2015-08-01). "Condorcet meets Bentham". Journal of Mathematical Economics. 59: 58–65. doi:10.1016/j.jmateco.2015.04.006.
Indeed, it is easy to construct examples where the Condorcet winner does not maximize social welfare [...however...] in a large population satisfying certain statistical regularities, not only is the Condorcet winner almost guaranteed to exist, but it is almost guaranteed to also be the utilitarian social choice.
- ↑ Lehtinen, Aki (2007-08-01). "The Welfare Consequences of Strategic Voting in Two Commonly Used Parliamentary Agendas". Theory and Decision. 63 (1): 1–40. CiteSeerX 10.1.1.727.3928. doi:10.1007/s11238-007-9028-4. ISSN 0040-5833. S2CID 153595828.
If the CW is not the same alternative as the utilitarian winner (UW), the latter ought to be selected according to the utilitarian welfare criterion
- ↑ G. Hägele and F. Pukelsheim (2001). "Llull's writings on electoral systems". Studia Lulliana. 41: 3–38.
- ↑ Colomer, Josep (2013). "Ramon Llull: From Ars Electionis to Social Choice Theory". Social Choice and Welfare. 40 (2): 317–328. doi:10.1007/s00355-011-0598-2. S2CID 43015882.
- ↑ Gehrlein, William V. (2011). Voting paradoxes and group coherence : the condorcet efficiency of voting rules. Lepelley, Dominique. Berlin: Springer. ISBN 9783642031076. OCLC 695387286.
empirical studies ... indicate that some of the most common paradoxes are relatively unlikely to be observed in actual elections. ... it is easily concluded that Condorcet's Paradox should very rarely be observed in any real elections on a small number of candidates with large electorates, as long as voters' preferences reflect any reasonable degree of group mutual coherence
- ↑ 6.0 6.1 Mackie, Gerry. (2003). Democracy defended. Cambridge, UK: Cambridge University Press. p. 6. ISBN 0511062648. OCLC 252507400.
- ↑ Nurmi, Hannu (2012), "On the Relevance of Theoretical Results to Voting System Choice", in Felsenthal, Dan S.; Machover, Moshé (eds.), Electoral Systems, Studies in Choice and Welfare, Springer Berlin Heidelberg, pp. 255–274, doi:10.1007/978-3-642-20441-8_10, ISBN 9783642204401, S2CID 12562825
- ↑ 8.0 8.1 Young, H. P. (1988). "Condorcet's Theory of Voting" (PDF). American Political Science Review. 82 (4): 1231–1244. doi:10.2307/1961757. ISSN 0003-0554. JSTOR 1961757. S2CID 14908863.
- ↑ Hogben, G. (1913). "Preferential Voting in Single-member Constituencies, with Special Reference to the Counting of Votes". Transactions and Proceedings of the Royal Society of New Zealand. 46: 304–308.
- ↑ Nanson, E. J. (1882). "Methods of election". Transactions and Proceedings of the Royal Society of Victoria. 19: 207–208.
although Ware's method cannot return the worst, it may return the next worst.
- ↑ McLean (2002), Australian electoral reform and two concepts of representation (PDF) (paper), UK: Ox, retrieved 2015-06-27
- ↑ "Wikimedia Foundation elections 2013/Results – Meta". meta.wikimedia.org. Retrieved 2017-01-23.
Further reading[change | change source]
- Black, Duncan (1958). The Theory of Committees and Elections. Cambridge University Press.
- Farquarson, Robin (1969). Theory of Voting. Oxford.
{{cite book}}: CS1 maint: location missing publisher (link) - Sen, Amartya Kumar (1970). Collective Choice and Social Welfare. Holden-Day. ISBN 978-0-8162-7765-0.
Other websites[change | change source]
- Johnson, Paul E, Voting Systems (PDF), Free faculty, retrieved 2015-06-27.
- Lanphier, Robert ‘Rob’, Condorcet's Method.
- Loring, Robert ‘Rob’, Accurate Democracy. The Basic Motions page lists Rules of Order for discussions and the motions organized on ranked choice ballots used in Condorcet voting.
- McKinnon, Ron, Condorcet Canada Initiative, CA, retrieved 2019-01-08. Multipage description of Condorcet method and Ranked Pairs from a Canadian perspective.
- Moulin, Hervé, Voting and Social Choice (PDF), NL: UVA, retrieved 2015-06-27. Demonstration and commentary on Condorcet method.
- Perez, Joaquin, A strong No Show Paradox is a common flaw in Condorcet voting correspondences (PDF), ES: UAH, archived from the original (PDF) on 2016-03-03, retrieved 2015-06-27.
- Prabhakar, Ernest (2010-06-28), Maximum Majority Voting (a Condorcet method), Radical centrism, retrieved 2015-06-27.
- Schulze, Markus, A New Monotonic, Clone-Independent, Reversal Symmetric, and Condorcet-Consistent Single-Winner Election Method (PDF).
Software[change | change source]
- CIVS, a free web poll service using the Condorcet method, Cornell.
- Condorcet PHP (Open-source command line application and PHP library for computing multiple Condorcet methods and others), 4 July 2022.
- Condorcet.Vote (A free web poll application using the original Condorcet method and many others like Schulze method.).
- Gorr, Eric, Condorcet Voting Calculator.
- STV (software for computing Condorcet methods and STV), Sourceforge.
- VoteFair surveys (Free ranking service that calculates Condorcet–Kemeny results), VoteFair
- VoteFair Ranking (Open-source C++ election software that calculates Condorcet–Kemeny results.), VoteFair, 25 September 2021
- Voteer (free web pool service using a Condorcet algorythme), Arpinum, archived from the original on 2019-07-16, retrieved 2020-05-08
- w.c.s. (A free web poll application using OpenSTV for voting algorithms), Entr'ouvert