Möbius strip


The Möbius strip or Möbius band, sometimes called a Mobius strip is a looped surface with only one side and only one edge. It can be made using a strip of paper by gluing the two ends together with a half-twist. The twisting is possible in two directions; so there are two different (mirror-image) Möbius strips.
The Mobius strip is known for its unusual properties. A bug crawling along the center line of the loop would go around twice before coming back to its starting point.[1] Cutting along the center line of the loop creates one longer band, not two. Cutting one third of the way in from the edge (and parallel to it) produces two Möbius strips, looped together.
The Möbius strip was discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in 1858.[2][3][4]
Mathematical description[change | change source]
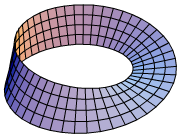

One way to represent the Möbius strip as a subset of can be done using the parametrization:
Where 0 ≤ α < 2π and −1 ≤ r ≤ 1. This creates a Möbius strip of width 1 whose center circle has radius 1, lies in the xy plane and is centered at (0, 0, 0). The parameter u runs around the strip while v moves from one edge to the other.
In cylindrical polar coordinates (r, θ, z), an unbounded version of the Möbius strip can be represented by the equation:
Topologically, the Möbius strip can be defined as the square [0,1] × [0,1] with its top and bottom sides identified by the relation (x, 0) ~ (1 − x, 1) for 0 ≤ x ≤ 1, as in the diagram on the right.
The Möbius strip is a two-dimensional compact manifold (i.e. a surface) with boundary. It is a standard example of a surface which is not orientable. The Möbius strip is also a standard example used to show the mathematical idea of a fiber bundle. Specifically, it is a nontrivial bundle over the circle S1 with a fiber the unit interval, I = [0,1]. Looking only at the edge of the Möbius strip gives a nontrivial two point (or Z2) bundle over S1.
A simple construction of the Möbius strip, which can be used to show it in computer graphics or modeling packages, is as follows:
- Take a rectangular strip. Rotate it around a fixed point not in its plane. At every step, also rotate the strip along a line in its plane (the line which divides the strip in two) and perpendicular to the main orbital radius. The surface generated on one complete revolution is the Möbius strip.
- Take a Möbius strip and cut it along the middle of the strip. This will form a new strip, which is a rectangle joined by rotating one end a whole turn. By cutting it down the middle again, this forms two interlocking whole-turn strips.
Möbius bands in nature and technology[change | change source]

There have been several technical applications for the Möbius strip. Giant Möbius strips have been used as conveyor belts. Such belts last longer because the entire surface area of the belt gets the same amount of wear. Möbius bands have also been used as continuous-loop recording tapes (to double the playing time). Möbius strips are common in the making of fabric computer printer and typewriter ribbons. There, they allow the ribbon to be twice as wide as the print head while using both half-edges evenly.
A device called a Möbius resistor is an electronic circuit element which has the property of canceling its own inductive reactance. Nikola Tesla patented similar technology in the early 1900s:[5] "Coil for Electro Magnets" was intended for use with his system of global transmission of electricity without wires.
The Möbius strip is the configuration space of two unordered points on a circle. Consequently, in music theory, the space of all two note chords, known as dyads, takes the shape of a Möbius strip.[6][7]
In physics/electro-technology:
- as compact resonator with the resonance frequency with half of identically constructed linear coils[8]
- as inductionless resistance[9]
- as superconductors with high transition temperature[10]

In chemistry/nano-technology:
- as “knot molecules” with special characteristics (Knotane [2], Chirality)
- as molecular engines[11]
- as graphene volume (nano-graphite) with new electronic characteristics, like helical magnetism[12]
- In a special type of aromaticity: Möbius aromaticity
- Charged particles, which were caught in the magnetic field of the earth, can move on a Möbius band[13]
- The cyclotide (cyclic protein) Kalata B1, active substance of the plant Oldenlandia affinis, contains Möbius topology for the peptide backbone.
Related pages[change | change source]
References[change | change source]
- ↑ Rainer Herges: Möbius, Escher, Bach – Das unendliche Band in Kunst und Wissenschaft. In: Naturwissenschaftliche Rundschau Wissenschaftliche Verlagsgesellschaft, p. 306, ISSN 0028-1050
- ↑ Clifford A. Pickover (March 2006). The Möbius Strip : Dr. August Möbius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology. Thunder's Mouth Press. ISBN 1560258268.
- ↑ Rainer Herges (2005-06-28). "Möbius, Escher, Bach – Das unendliche Band in Kunst und Wissenschaft". Naturwissenschaftliche Rundschau. pp. 301–310. ISSN 0028-1050.
{{cite book}}:|journal=ignored (help) - ↑ Chris Rodley, ed. (1997). Lynch on Lynch. London, Boston. p. 231.
{{cite book}}: CS1 maint: location missing publisher (link) - ↑ U.S. Patent 512,340
- ↑ Clara Moskowitz, Music Reduced to Beautiful Math, LiveScience
- ↑ Dmitri Tymoczko (7 July 2006). "The Geometry of Musical Chords". Science. 313 (5783): 72–74. Bibcode:2006Sci...313...72T. doi:10.1126/science.1126287. PMID 16825563. S2CID 2877171.
- ↑ IEEE of Trans. Microwave Theory and Tech., volume. 48, No. 12, pp. 2465–2471, Dec. 2000
- ↑ U.S. Patent 3.267.406
- ↑ Raul Perez Enriquez A Structural parameter for High Tc Superconductivity from an Octahedral Moebius Strip in RBaCuO: 123 type of perovskite Rev Mex Fis v.48 supplement 1, 2002, p.262 or at here
- ↑ Angew Chem Int OD English one 2005 February 25; 44 (10): 1456–77.
- ↑ arXiv: cond-mat/0309636 v1 Physica E 26 February 2006
- ↑ IEEE Transactions on plasma Science, volume. 30, No. 1, February 2002





