Decagon

A decagon is a shape with 10 sides and 10 corners.
Regular decagon[change | change source]
All sides of a regular decagon are the same length. Each corner is 144°. All corners added together equal 1440°.
Area[change | change source]
The amount of space a regular decagon takes up is
a is the length of one of its sides.
An alternative formula is where d is the distance between parallel sides, or the height when the decagon stands on one side as base.
By simple trigonometry .
Sides[change | change source]
The side of a regular decagon inscribed in a unit circle is , where ϕ is the golden ratio, .
Dissection of regular decagon[change | change source]
Coxeter states that every parallel-sided 2m-gon can be divided into m(m-1)/2 rhombs. For the regular decagon, m=5, and it can be divided into 10 rhombs, with examples shown below. This decomposition can be seen as 10 of 80 faces in a Petrie polygon projection plane of the 5-cube. A dissection is based on 10 of 30 faces of the rhombic triacontahedron.[1] The list A006245 defines the number of solutions as 62, with 2 orientations for the first symmetric form, and 10 orientations for the other 6.
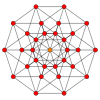 5-cube |
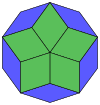
|

|
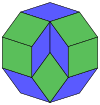
|

|

|

|
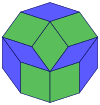
|
Skew decagon[change | change source]
| {5}#{ } | {5/2}#{ } | {5/3}#{ } |
|---|---|---|
|
|

|
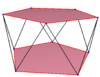
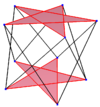
| A regular skew decagon is seen as zig-zagging edges of a pentagonal antiprism, a pentagrammic antiprism, and a pentagrammic crossed-antiprism. | ||
A skew decagon is a skew polygon with 10 vertices and edges but not existing on the same plane. The interior of such an decagon is not generally defined. A skew zig-zag decagon has vertices alternating between two parallel planes.
A regular skew decagon is vertex-transitive with equal edge lengths. In 3-dimensions it will be a zig-zag skew decagon and can be seen in the vertices and side edges of a pentagonal antiprism, pentagrammic antiprism, and pentagrammic crossed-antiprism with the same D5d, [2+,10] symmetry, order 20.
These can also be seen in these 4 convex polyhedra with icosahedral symmetry. The polygons on the perimeter of these projections are regular skew decagons.
 Dodecahedron |
 Icosahedron |
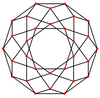 Icosidodecahedron |
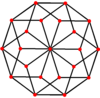 Rhombic triacontahedron |
Related pages[change | change source]
- Decagonal number and centered decagonal number, figurate numbers modeled on the decagon
- Decagram, a star polygon with the same vertex positions as the regular decagon
References[change | change source]
Other websites[change | change source]
- Eric W. Weisstein, Decagon at MathWorld.
- Definition and properties of a decagon With interactive animation






