Pentacontagon
| Regular pentacontagon | |
|---|---|
 A regular pentacontagon | |
| Type | Regular polygon |
| Edges and vertices | 50 |
| Schläfli symbol | {50}, t{25} |
| Coxeter diagram | |
| Symmetry group | Dihedral (D50), order 2×50 |
| Internal angle (degrees) | 172.8° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a pentacontagon or pentecontagon or 50-gon is a fifty-sided polygon.[1][2] The sum of any pentacontagon's interior angles is 8640 degrees.
Regular pentacontagon[change | change source]
A regular pentacontagon is represented by Schläfli symbol {50} and can be constructed as a quasiregular truncated icosipentagon, t{25}, which alternates two types of edges.
Area[change | change source]
One interior angle in a regular pentacontagon is 1724⁄5°, meaning that one exterior angle would be 71⁄5°.
The area of a regular pentacontagon is (with t = edge length)
and its inradius is
The circumradius of a regular pentacontagon is
Since 50 = 2 × 52, a regular pentacontagon is not constructible using a compass and straightedge,[3] and is not constructible even if the use of an angle trisector is allowed.[4]
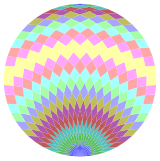
Dissection[change | change source]

Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms.[5] In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular pentacontagon, m=25, it can be divided into 300: 12 sets of 25 rhombs. This decomposition is based on a Petrie polygon projection of a 25-cube.
|

|

|

|
References[change | change source]
- ↑ Gorini, Catherine A. (2003). The Facts on File Geometry Handbook. Infobase Publishing. p. 120. ISBN 978-1-4381-0957-2.
- ↑ Peirce, Charles Sanders (1976). The New Elements of Mathematics: Algebra and geometry. Mouton Publishers. p. 298. ISBN 9780391006126.
- ↑ Constructible Polygon
- ↑ "Archived copy" (PDF). Archived from the original (PDF) on 2015-07-14. Retrieved 2015-02-19.
{{cite web}}: CS1 maint: archived copy as title (link) - ↑ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
- Eric W. Weisstein, Pentacontagon at MathWorld.
- Naming Polygons and Polyhedra
- Finkel, Benjamin Franklin (1888). A Mathematical Solution Book Containing Systematic Solutions to Many of the Most Difficult Problems: Taken from the Leading Authors on Arithmetic and Algebra, Many Problems and Solutions from Geometry, Trigonometry and Calculus, Many Problems and Solutions from the Leading Mathematical Journals of the United States, and Many Original Problems and Solutions. Kibler.




